ज्यामिति (Geometry)

Description

ज्यामिति (Geometry) गणित की एक शाखा है जो आकृतियों, आकारों, स्थिति (position) और अंतरिक्ष में वस्तुओं के गुणों का अध्ययन करती है। यह गणित की सबसे पुरानी शाखाओं में से एक है और इसका नाम ग्रीक शब्दों "geo" (भूमि) और "metron" (मापन) से आया है, जिसका अर्थ है "भूमि का मापन"।

सरल शब्दों में, ज्यामिति हमें यह समझने में मदद करती है कि हमारे आस-पास की दुनिया कैसे बनी है। यह हमें यह समझने के लिए नियम देती है कि बिंदु (points), रेखाएँ (lines), कोण (angles) और विभिन्न आकृतियाँ (shapes) एक-दूसरे से कैसे संबंधित हैं।

मुख्य अवधारणाएँ (Key Concepts)

• बिंदु (Point): यह ज्यामिति की सबसे बुनियादी इकाई है। यह अंतरिक्ष में एक स्थिति को दर्शाता है और इसका कोई आयाम (dimension) नहीं होता।

   

   

• रेखा (Line): बिंदुओं का एक समूह जो दोनों दिशाओं में अनंत (infinitely) तक फैलता है।

   

   

• समतल (Plane): एक सपाट, द्वि-आयामी सतह जो सभी दिशाओं में अनंत तक फैलती है।

   

   

• आकृतियाँ (Shapes):

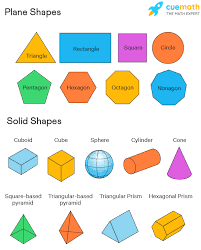
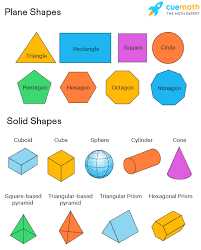
  • द्वि-आयामी (2D) आकृतियाँ: ये सपाट आकृतियाँ हैं जैसे त्रिभुज (triangle), वर्ग (square), और वृत्त (circle)। इनका क्षेत्रफल (area) होता है लेकिन आयतन (volume) नहीं होता।

  • त्रि-आयामी (3D) आकृतियाँ: ये ठोस आकृतियाँ हैं जैसे घन (cube), गोला (sphere), और पिरामिड (pyramid)। इनका आयतन होता है।

• कोण (Angle): दो प्रतिच्छेदी (intersecting) रेखाओं या किरणों के बीच का स्थान।

   

   

• प्रमेय (Theorems): ज्यामिति में स्थापित नियम हैं जो हमेशा सत्य होते हैं। इसका सबसे प्रसिद्ध उदाहरण पाइथागोरस प्रमेय (Pythagorean Theorem) है, जो समकोण त्रिभुजों की भुजाओं के बीच संबंध बताता है।

ज्यामिति की मुख्य शाखाएँ (Main Branches of Geometry)

• यूक्लिडियन ज्यामिति (Euclidean Geometry): यह सबसे आम प्रकार की ज्यामिति है जो स्कूल में सिखाई जाती है। यह समतल सतहों और 3D अंतरिक्ष के साथ काम करती है। यह सीधी रेखाओं और समानांतर रेखाओं (parallel lines) जैसे अवधारणाओं पर आधारित है।

   

   

• विश्लेषणात्मक ज्यामिति (Analytical Geometry): यह बीजगणित और ज्यामिति को एक साथ जोड़ती है। इसमें आकृतियों और समीकरणों का अध्ययन करने के लिए निर्देशांक प्रणाली (coordinate system) (जैसे कार्टेशियन निर्देशांक) का उपयोग किया जाता है।

   

   

• गैर-यूक्लिडियन ज्यामिति (Non-Euclidean Geometry): यह एक उन्नत शाखा है जो घुमावदार सतहों (curved surfaces) का अध्ययन करती है। इसका उपयोग अल्बर्ट आइंस्टीन के सापेक्षता के सिद्धांत (theory of relativity) जैसी भौतिकी (physics) की शाखाओं में होता है।

   

   

ज्यामिति क्यों महत्वपूर्ण है?

ज्यामिति केवल एक स्कूल का विषय नहीं है, बल्कि यह हमारे दैनिक जीवन में बहुत उपयोगी है:

• वास्तुकला और इंजीनियरिंग: इमारतों, पुलों और सड़कों को डिज़ाइन करने के लिए।

• कला और डिज़ाइन: चित्रों, मूर्तियों और ग्राफिक डिज़ाइन को बनाने के लिए।

• विज्ञान: भौतिकी में ग्रहों की गति को समझने के लिए, और कंप्यूटर ग्राफिक्स में 3D मॉडल बनाने के लिए।

• दैनिक जीवन: किसी वस्तु के आकार, दूरी, और स्थिति का अनुमान लगाने के लिए।

ज्यामिति को सीखने का सबसे अच्छा तरीका आकृतियों को बनाना और समस्याओं को हल करना है। इससे आप इसके नियमों को बेहतर ढंग से समझ पाएंगे।