ALGEBRA

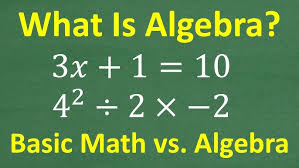
Description

बीजगणित (Algebra) गणित की एक शाखा है जो अंकगणित (arithmetic) को सामान्य बनाती है। यह अज्ञात (unknown) राशियों और संबंधों को दर्शाने के लिए प्रतीकों (symbols) - आमतौर पर x या y जैसे अक्षरों - का उपयोग करने की कला है। यह आपको समस्याओं को हल करने, वास्तविक दुनिया की स्थितियों को model करने और ऐसे सार्वभौमिक नियमों को व्यक्त करने की अनुमति देता है जो किसी भी संख्या के लिए सत्य होते हैं।

उदाहरण के लिए, "3 और किसी संख्या का जोड़ 7 है" कहने के बजाय, बीजगणित आपको इसे और अधिक कुशलता से $3+x=7$ लिखने और फिर अज्ञात राशि (x) के लिए व्यवस्थित रूप से हल करने देता है, जिसका मान $x=4$ है।

मुख्य अवधारणाएँ (Key Concepts)

इन मुख्य विचारों को समझना बीजगणित में महारत हासिल करने का पहला कदम है:

• चर (Variables): ये वे अक्षर या प्रतीक हैं जो अज्ञात मानों (unknown values) को दर्शाते हैं। ये "चर" (variable) हैं क्योंकि इनका मान हर समस्या में बदल सकता है।

• अचर (Constants): ये स्थिर संख्याएँ हैं, जैसे 5, −10, या π । इनका मान कभी नहीं बदलता।

• व्यंजक (Expressions): यह चर, अचर और गणितीय संक्रियाओं (operations) का एक समूह है जो एक गणितीय वाक्यांश बनाता है। उदाहरण के लिए, $5x+3y-7$ एक व्यंजक है।

• समीकरण (Equations): यह एक कथन है कि दो व्यंजक बराबर हैं, जो बराबर चिह्न (=) से जुड़े होते हैं। इसका लक्ष्य अक्सर चर के उस मान को खोजना होता है जो समीकरण को सत्य बनाता है। उदाहरण के लिए, $2x+5=11$।

• असमिकाएँ (Inequalities): यह एक कथन है जो > (से बड़ा), < (से छोटा), ≥ (से बड़ा या बराबर), या ≤ (से छोटा या बराबर) जैसे प्रतीकों का उपयोग करके दो व्यंजकों की तुलना करता है। उदाहरण के लिए, $x-3>5$।

• गुणांक (Coefficients): यह वह संख्या है जो किसी पद (term) में एक चर से गुणा होती है। पद 4x में, 4 गुणांक है।

बीजगणित की मुख्य शाखाएँ (Main Branches of Algebra)

बीजगणित सिर्फ एक विषय नहीं है; यह विभिन्न स्तरों की जटिलता और विशेषज्ञता वाला एक विशाल क्षेत्र है।

• प्रारंभिक बीजगणित (Elementary Algebra): यह बीजगणित का वह रूप है जिसे ज़्यादातर लोग सबसे पहले सीखते हैं। इसमें रैखिक (linear) और द्विघात (quadratic) समीकरणों को हल करना, बहुपदों (polynomials) के साथ काम करना, और चर और व्यंजक जैसी बुनियादी अवधारणाओं को समझना शामिल है।

• रैखिक बीजगणित (Linear Algebra): यह शाखा सदिशों (vectors), मैट्रिसेस (matrices) और रैखिक परिवर्तनों (linear transformations) पर केंद्रित है। यह कंप्यूटर ग्राफिक्स, डेटा साइंस, भौतिकी और इंजीनियरिंग जैसे क्षेत्रों के लिए महत्वपूर्ण है। यह आपको एक साथ कई चरों वाले समीकरणों की प्रणालियों को हल करने की अनुमति देता है।

• अमूर्त बीजगणित (Abstract Algebra): यह एक बहुत ही उन्नत क्षेत्र है जो समूहों (groups), वलयों (rings) और क्षेत्रों (fields) जैसी अमूर्त गणितीय संरचनाओं का अध्ययन करता है। यह किसी विशिष्ट संख्या को हल करने के बजाय इन संरचनाओं के गुणों को समझने के बारे में है।

• बूलियन बीजगणित (Boolean Algebra): यह बीजगणित का एक विशेष प्रकार है जो बाइनरी चरों (true/false, 1/0) और AND, OR, और NOT जैसे तार्किक संक्रियाओं (logical operations) से संबंधित है। यह कंप्यूटर विज्ञान और डिजिटल सर्किट की मूल भाषा है।

बीजगणित को प्रभावी ढंग से कैसे सीखें

1. मूलभूत बातों से शुरुआत करें: बुनियादी अवधारणाओं को न छोड़ें। समीकरणों को हल करने से पहले सुनिश्चित करें कि आप चरों, अचरों और गणितीय संक्रियाओं के क्रम (BODMAS) को पूरी तरह से समझ लें।

2. अभ्यास, अभ्यास, अभ्यास: बीजगणित केवल ज्ञान नहीं, बल्कि एक कौशल है। बेहतर होने का एकमात्र तरीका विभिन्न प्रकार की समस्याओं को हल करना है। सरल समीकरणों से शुरू करें और धीरे-धीरे कठिनाई बढ़ाएं।

3. "क्यों" को समझें: केवल सूत्रों या नियमों को याद न करें। हर संक्रिया के पीछे के तर्क को समझने की कोशिश करें। उदाहरण के लिए, जब आप "दोनों पक्षों से 5 घटाते हैं," तो आप केवल एक नियम का पालन नहीं कर रहे होते हैं; आप समीकरण का संतुलन बनाए रख रहे होते हैं।

4. कल्पना करें (Visualize): समीकरणों और असमानताओं को देखने के लिए आरेख (diagrams) बनाएँ, संख्या रेखाओं (number lines) का उपयोग करें, या ग्राफ प्लॉट करें। इससे अमूर्त अवधारणाओं को समझना बहुत आसान हो सकता है।