Trigonmetry

Description

. The Foundation: ज़रूरी ज्ञान

Trigonometry (त्रिकोणमिति) सीखने से पहले, इन बुनियादी चीज़ों को समझना बहुत ज़रूरी है:

• Algebra (बीजगणित): समीकरणों (equations) को हल करना, variables (चर) को manipulate करना, और exponents (घातांक) और radicals (करणी) के साथ काम करना आपको अच्छे से आना चाहिए।

• Geometry (ज्यामिति): आपको बुनियादी ज्यामितीय आकृतियाँ, खासकर त्रिभुज (triangles) की अच्छी समझ होनी चाहिए। आपको Pythagoras Theorem (पाइथागोरस प्रमेय), त्रिभुजों के गुण (खासकर समकोण त्रिभुज - right-angled triangles), और कोणों (angles) और डिग्री (degrees) की अवधारणाओं से परिचित होना चाहिए।

2. The Core Concepts: मुख्य अवधारणाएँ

छोटे-छोटे कदमों से शुरुआत करें और अपना ज्ञान धीरे-धीरे बढ़ाएं।

चरण 1: समकोण त्रिभुज (Right-Angled Triangles)

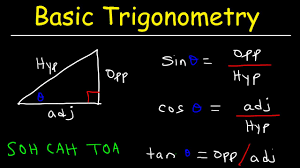
• समकोण त्रिभुज का परिचय: तीनों भुजाओं (sides) को समझें: कर्ण (hypotenuse - सबसे लंबी भुजा, समकोण के सामने), लंब (opposite side), और आधार (adjacent side) (एक specific angle के सापेक्ष)।

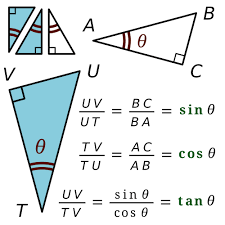
• छह त्रिकोणमितीय अनुपात (Trigonometric Ratios): तीन मुख्य अनुपातों (ratios) की परिभाषा सीखें:

  • Sine (sin): sin(θ)=कर्णलंब​

  • Cosine (cos): cos(θ)=कर्णआधार​

  • Tangent (tan): tan(θ)=आधारलंब​

  • याद करने का तरीका: \\\"लाल/कक्का\\\" (Lal/Kakka) या \\\"पंडित बद्री प्रसाद, हर हर बोले\\\" (Pandit Badri Prasad, Har Har Bole) जैसे mnemonics का उपयोग करें।

• व्युत्क्रम अनुपात (Reciprocal Ratios): अन्य तीन अनुपातों को सीखें, जो मुख्य तीन के व्युत्क्रम (reciprocals) हैं:

  • Cosecant (csc): csc(θ)=sin(θ)1​=लंबकर्ण​

  • Secant (sec): sec(θ)=cos(θ)1​=आधारकर्ण​

  • Cotangent (cot): cot(θ)=tan(θ)1​=लंबआधार​

• अभ्यास: समकोण त्रिभुजों की भुजाओं और कोणों को खोजने वाले कई प्रश्नों को हल करें।

चरण 2: समकोण त्रिभुज से आगे बढ़ना

• इकाई वृत्त (The Unit Circle): यह एक fundamental concept है जो trigonometry को समकोण त्रिभुजों से आगे बढ़ाता है।

  • इकाई वृत्त को समझना: यह एक ऐसा वृत्त है जिसकी त्रिज्या 1 है और जो coordinate plane (निर्देशांक समतल) के मूल बिंदु (origin) पर केंद्रित है।

  • अनुपातों से संबंध: वृत्त पर किसी भी बिंदु (x,y) के निर्देशांक (coordinates) कोण θ से इस तरह संबंधित हैं: x=cos(θ) और y=sin(θ).

  • अभ्यास: इकाई वृत्त का उपयोग करके 0∘,30∘,45∘,60∘,90∘ और उनके गुणजों (multiples) के sine, cosine, और tangent का मान खोजना सीखें। इससे आपको यह भी समझने में मदद मिलेगी कि विभिन्न quadrants (चतुर्थांशों) में इन functions के चिन्ह (signs) कैसे बदलते हैं।

• रेडियन माप (Radian Measure): कोणों को मापने के लिए डिग्री के विकल्प के रूप में रेडियन के बारे में जानें। conversion को समझें: 180∘=π रेडियन।

चरण 3: सर्वसमिकाएँ और समीकरण (Identities and Equations)

• त्रिकोणमितीय सर्वसमिकाएँ (Trigonometric Identities): ये ऐसे समीकरण हैं जो variables के सभी मानों के लिए सत्य होते हैं।

  • पाइथागोरस सर्वसमिकाएँ: सबसे महत्वपूर्ण है sin2(θ)+cos2(θ)=1. इससे अन्य दो को प्राप्त करना सीखें।

  • जोड़ और घटाव के सूत्र (Sum and Difference Formulas): sin(A±B), cos(A±B), और tan(A±B) के सूत्र सीखें।

  • दोहरे कोण के सूत्र (Double Angle Formulas): sin(2θ), cos(2θ), और tan(2θ) के सूत्र सीखें।

• त्रिकोणमितीय समीकरणों को हल करना: सर्वसमिका और इकाई वृत्त के अपने ज्ञान का उपयोग करके किसी दिए गए समीकरण को संतुष्ट करने वाले कोणों के मानों को खोजें।

चरण 4: अनुप्रयोग और उन्नत विषय (Applications and Advanced Topics)

• गैर-समकोण त्रिभुजों को हल करना:

  • Sine का नियम (Law of Sines): इसका उपयोग लापता भुजाओं या कोणों को खोजने के लिए करें जब आपके पास एक कोण और उसकी सामने की भुजा का जोड़ा हो।

  • Cosine का नियम (Law of Cosines): इसका उपयोग तब करें जब आपके पास या तो तीनों भुजाएं (SSS) हों या दो भुजाएं और उनके बीच का कोण (SAS) हो।

• त्रिकोणमितीय functions का ग्राफ बनाना: y=sin(x), y=cos(x), और y=tan(x) के ग्राफ बनाना सीखें। आयाम (amplitude), अवधि (period), phase shift, और vertical shift जैसी अवधारणाओं को समझें।

3. प्रभावी सीखने की रणनीतियाँ

• सक्रिय शिक्षण (Active Learning): सिर्फ पढ़ें नहीं, अभ्यास करें! जितना हो सके उतने प्रश्नों को हल करें।

• कल्पना करें (Visualize): अवधारणाओं को कल्पना करने के लिए आरेखों और इकाई वृत्त का उपयोग करें। त्रिभुज और कोणों को बनाएं।

• फ्लैशकार्ड्स (Flashcards): सर्वसमिका और सूत्रों के लिए फ्लैशकार्ड बनाएं। उन्हें याद करें, लेकिन यह भी समझें कि वे कैसे प्राप्त होते हैं।

• नियमित रूप से दोहराएं (Review Regularly): त्रिकोणमिति की अवधारणाएं एक-दूसरे पर आधारित होती हैं। उन्हें ताज़ा रखने के लिए पुराने material को नियमित रूप से दोहराएं।